Физика шаровой молнии.
(Статья временно повреждена. Ведётся восстановление.)
Попов А.Ф.
Сухумский физико-технический институт. г. Сухум. Республика Абхазия.
В данной работе(1) приведено обоснование плазменной модели природы шаровой молнии. В основе предлагаемой модели лежит теоретически предсказанная бессиловая магнитная конфигурация – сферомак. Зарождается она в канале линейной молнии при повторных разрядах в областях развития на нём неустойчивости типа перетяжек. Начальным полоидальным магнитным полем служит слабое магнитное поле Земли. В процессе сжатия токовой оболочки полоидальное магнитное поле возрастает и становится сравнимым с азимутальным магнитным полем пинча. В результате перезамыкания силовых линий полоидального магнитного поля в области перетяжек образуются бессиловые магнитные конфигурации с замкнутым магнитным полем, которые и являются основой шаровой молнии. В зависимости от числа слившихся бессиловых ячеек энергия и размеры шаровой молнии могут изменяться в широких пределах. Во внешней области, за сеперетрисой, силовые линии магнитного поля незамкнуты и уходят в бесконечность. Основная энергия в ней запасена в виде энергии магнитного поля.
На границе с воздухом образуется тонкая оболочка неизотермической плазмы. В ней по внутренней к сепаратисе поверхности протекает диамагнитный ток, экранирующий её от магнитного поля плазмоида. На внешней поверхности оболочки неизотермической плазмы возникает двойной электрический слой, являющийся потенциальным барьером для электронов. В результате интенсивной конденсации паров воды на отрицательных и положительных ионах в воздухе на границе двойного слоя образуется водяная плёнка. Молекулы воды играют также важную роль в образовании кластеров в двойном электрическом слое, в результате чего существенно снижается величина и энергия потока ионов. Кроме того, неизотермическая плазма оболочки служит отражательным экраном для интенсивного циклотронного излучения электронов из центральной бессиловой области. В целом, внешняя оболочка молнии является эффективным тепловым и магнитным экраном. Вследстивии сильного электростатического давления в двойном электрическом слое плотность энергии в шаровой молнии достигает порядка 10 Дж/см3.
Основные свойства шаровой молнии удовлетворительно описываются в рамках данной модели.
Попытки объяснения природы шаровой молнии на основе представления физики плазмы предпринимались неоднократно [2,3]. Уже на ранних этапах исследований высказывались предположения, что шаровая молния образуется во время грозового разряда из участка канала линейной молнии [4]. Однако шаровая молния на плазменной основе имела низкую плотность энергии и слишком малый вес. Непреодолимой на первый взгляд, казалась проблема сопряжения горячего вещества молнии с окружающим ее холодным воздухом. Тем не менее, более тщательный анализ физических процессов на границе шаровой молнии показывает, что эти недостатки не принципиальны и при определенных условиях устранимы.
I. Магнитное поле автономного плазмоида.
Учитывая выше сказанное, достаточно разумным является предположение, что шаровая молния образуется из отрезка канала линейной молнии при развитии на нем перетяжечной неустойчивости. Известно, что достижение равновесия в отрезке плазменного цилиндра с продольным током возможно только при наличии магнитного поля направленного вдоль тока. Конечное достаточно большой напряженности продольное магнитное поле при грозовом разряде может образоваться при сильном сжатии плазменного канала вместе с "вмороженным" в него слабым магнитным полем Земли. Первоначально усиление продольного магнитного поля происходит вследствие сохранения магнитного потока в проводящей среде. В процессе сжатия плазменного отрезка канала в результате кумуляции сходящейся к оси ударной волны плазма нагревается до сотни миллионов градусов [6]. Высокотемпературная плазма обладает высокой проводимостью, однако, при однородном давлении в шнуре ток может протекать только вдоль силовых линий магнитного поля. Поэтому при выравнивании давления в отраженной от оси ударной волне происходит дальнейшее усиление полоидального магнитного поля. Действительно, если пренебречь инерцией, то плотность тока в замагниченной плазме равна выражению [7]
Формула ст, 3
Вследствие выравнивания давления за фронтом отраженной ударной волны первоначальный ток в шнуре не может быть им обеспечен. Поэтому можно считать, что распространение отраженной ударной волны сопровождается срывом перпендикулярной магнитному полю составляющей первоначального тока проводимости и генерацией тока смещения.
Непосредственно индуцированное электрическое поле в бесстолкновительной плазме не вызывает заметного поперечного тока. Лишь редкие столкновения электронов приводят к их смещению вдоль вектора поля. Поскольку первоначально электроны дрейфуют относительно ионов, то в плазме возникает ток приводящий к разделению зарядов и образованию радиального электрического поля в плазменном шнуре. Очевидно, что максимальная напряженность этого поля будет равна напряженности холловского электрического поля [7]
Формула ст.4
Эффективное электрическое поле, -плотность и давление электронов плазмы, соответственно, и ƠJ-величина исчезающего тока, которая восстановит поперечный ток в плазме. Однако если ионы замагничены, то они за время ионного циклотронного периода также выходят в дрейф и холловский ток исчезает. В результате учета инерции частиц получим, что индуцированное нестационарное электрическое поле вызывает в замагниченной плазме поляризационный ток [8]
Формула ст.4
который и дает основной вклад в поперечный ток пинча. Для поддержания поляризационного тока расходуется энергия магнитного поля, создаваемого поперечным током, и плазма в этом процессе дрейфует в скрещенных электрическом и магнитном полях. Вследствие свободного вытекания плазмы из области перетяжки дрейф не может привести к образованию заметного градиента давления в этой области и к восстановлению поперечной проводимости. Плазма стремится к бес силовому состоянию. Из выражений (I) и (3) следует, что в этом процессе полоидальная компонента тока убивает, а азимутная растет, поскольку вклад поперечного тока в эти компоненты противоположного знака. Таким образом, за фронтом отраженной ударной волны происходит увеличение напряженности полоидального магнитного поля. В результате перезамыкания силовых линий полоидального магнитного поля во внешней области перетяжки происходит отключение участка канала и образование конфигурации с замкнутым током (Рис.1). При малом давлении плазмы по сравнению с давлением магнитного поля результирующая магнитная конфигурация является бессиловой. Натяжение тороидального магнитного поля в ней сдерживается противодавлением полоидального магнитного поля.
Очевидно, что активность плазмы на этом этапе не заканчивается. Так под действием теплового расширения бессиловые конфигурации сближаются и начинается процесс их слияния (Рис.2). Вследствие малости давления плазмы по сравнению с давлением магнитного поля оно может воспрепятствовать сближению противоположно направленных полоидальных магнитных полей, а свободное растекание плазмы вдоль линий магнитного поля не позволяет возникновению в этой области сколь-нибудь существенного градиента давления и, следовательно, значительного тока поперек магнитного поля. При сближении магнитных конфигураций в результате взаимной индукции в смежных областях тороидального электрического поля усиливается, а напряженность полоидального электрического поля уменьшается. Вектор электрического поля получает приращение в направлении перпендикулярном вектору магнитного поля. Поскольку ток течет только вдоль силовых линий магнитного поля и его плотность равна выражению (1), то модуль плотности тока j = ơEcosφ, где φ - угол между векторами E и H, и он меньше величины плотности тока в среде с изотропной проводимостью (j=ơE), необходимой для поддержания магнитного поля. Поэтому процесс слияния сферомаков должен сопровождаться более сильной индукцией электрического поля.
Компоненты полоидальной и тороидальной плотности тока даются выражениями
Jp=ơ {(E-pH) + E H } /H Формула стр.5
Они независимы при форм. Если не выполняется это условие в плазме индуцируется электрическое поле не параллельное магнитному полю и магнитные потоки оказываются связанными. В этом случае возможна как различная скорость диссипации потоков, так и усиление магнитного поля одного потока за счет энергии другого.
Из симметрии задачи следует, что в точках соприкосновения сферомаков формула и следовательно . Совокупность точек соприкосновения образуют окружность радиуса ггггггггггг c центром на оси симметрии. Вдоль силовой линии тороидального магнитного поля, проходящей через точки соприкосновения, потечет ток с плотностью J формула В результате увеличения тока в окрестности этой силовой линии создается дополнительное магнитное поле H۹ ., которое изменяет топологию полоидального магнитного поля в смежных областях сферомаков. Изменение распределения полоидального магнитного поля показана на Рис.2. По мере сближения сферомаков радиус токового кольца изменяется от нуля до радиуса магнитной оси конечного сферомака.
В связи с генерацией дополнительного магнитного поля равновесие нарушается и сила формула обеспечивает стягивание двух смежных сферомаков к вновь образовавшейся магнитной оси. В то же время сила формула в плоскости соприкосновения направлена в разные стороны от токового кольца в радиальном направлении. Очевидно, что под действием этих сил система из цепочки сферомаков стремится к конечному сферомаку радиуса R, если внешние силы не препятствуют этому.
При погружении сферомака, заполненного высокотемпературной плазмой, в атмосферу налетающий на него нейтральный газ ионизуется на некотором расстоянии от него и отражается магнитным полем сгустка. В результате в граничном слое вновь образованной плазмы возникает ток, который экранирует внешнюю область от магнитного поля сгустка. В замагниченной плазме большая часть электронов отражается магнитным полем в переходном слое и только незначительное количество электронов испытывает столкновения с ионами и диффундирует во внутрь переходного слоя. В случае, когда свободный пробег электрона больше характерной длины силовой линии магнитного поля, захваченные частицы уходят из переходного слоя вдоль силовых линий. Очевидно, что толщина переходного слоя при этих условиях порядка циклотронного радиуса электрона. Давление внешней плазмы в данном случае уравновешивается давлением магнитного поля формула напряженность магнитного поля на границе бессиловой области.
Формирование внешнего магнитного поля плазмоида происходит следующим образом. Вследствие медленной диффузии замагниченной плазмы поперек магнитного поля и ее свободного растекания вдоль силовых линий магнитного поля первоначально вблизи полюсов диамагнитный ток протекает по воронкообразной поверхности с горловиной направленной к центру плазмоида. В результате перезамыкания силовых линий магнитного поля, генерируемого этим током в горловине, и полоидального поля сгустка при последующем выпрямлении силовых линий образуется внешнее магнитное поле. Вследствие увеличения его напряженности по сравнению с полем классического сферомака бессиловая область плазмоида деформируется и ее форма, по-видимому, будет близка к форме сплюснутого эллипсоида вращения (Рис.3). Силовые линии внешнего магнитного поля незамкнуты и уходят в бесконечность, быстро убывая при удалении от сгустка. Таким образом, магнитное поле плазмоида в атмосфере поддерживается собственными токами и не требует посторонних источников. Шаровая молния является полностью автономной системой.
2. Термоизоляция высокотемпературного плазмоида.
Поскольку на внешней границе сгусток плазмы соприкасается с холодным окружающим газом, то в этой области термоизоляция плазмы может быть осуществлена только двойным электрическим слоем, возникающим благодаря более высокой подвижности электронов по сравнению с ионами [9]. В атмосфере низко энергичные электроны, преодолевшие потенциальный барьер, эффективно прилипают к электроотрицательным атомам, образуя малоподвижный отрицательный ион. Двойной электрический слой не может ограничить потери тепловой энергии ионной компоненты, поэтому температура ионов во внешней плазменной оболочке близка к температуре холодного газа при высокой электронной температуре. В случае, когда пробег электронов значительно больше толщины двойного слоя, а для ионов выполняется обратное условие, плотности электронного и ионного потоков в слое определяются выражениями формула соответственно, где E - напряженность электрического поля в слое и время рассеяния ионов. Равенством потоков на внешней границе определяется разность потенциалов в двойном слое.
Формула
Разность потенциалов в слое зависит от величины времени рассеяния ионов. При малых разность потенциалов может достигать порядка десятка величин
Ионы при своем движении в электрическом поле двойного слоя испытывают столкновения как с нейтральными атомами, так и с положительными и отрицательными ионами. При низких температурах вклад столкновений с ионами является основным, поскольку эффективное сечение для кулоновских столкновений велико. Так при Т ~5000 к и Z=1 Процесс движения ионов в электрическом поле сопровождается выделением тепла в двойном слое. При тепловая скорость иона, кинетическая энергия иона определяется температурой газа. Относительно невелика также передача энергии ионами от горячего электронного газа, поскольку в каждом акте столкновения из-за различия их масс доля передаваемой энергии порядка
И сечение кулоновского столкновения мало при высокой электронной температуре.
Из предыдущего анализа следует, что электронный поток в окружающей сгусток газ ослабевает пропорционально формула Тем не менее в плотной плазме даже при фформм переносимая ими энергия все еще велика. В действительности в ограниченной плазме эти потери могут быть существенно меньше, поскольку электроны с энергией фаоовов ,где оаововоо нормальная к границе компонента скорости электрона, преодолевают потенциальный барьер и уходят в окружающую среду. Поскольку в слое присутствуют в достаточно большом количестве молекулы воды и тяжелые кластеры, на которых электроны испытывают быстрое угловое рассеяние, то в этом случае в слое должны отсутствовать электроны с энергией, превышающей Только в результате кулоновских столкновений устанавливается небольшой поток частиц в эту область энергий, который и определяет величину плотности электронного потока S из слоя неизотермической плазмы. По порядку величины где фол лволвл время кулоновского рассеяния электронов толщина оболочки неизотермической плазмы. В стационарных условиях этот поток будет уносить энергию, получаемую внешней плазмой в результате ее нагрева в интенсивном циклотронном излучении электронов из центральной области.
Наличие паров воды в газе существенно улучшает термоизолирующие свойства двойного слоя, как и его устойчивость, поскольку внешняя низкотемпературная плазма из положительных и отрицательных ионов в окрестности сгустка представляет собой благоприятную среду для образования комплексных ионов - кластеров. Молекулы воды, обладающие большим дипольным электрическим моментом, притягиваются к ионам, образуя устойчивые оболочки вокруг них [3]. При малом потоке энергии в область ионной плазмы, когда тепло из нее может отводится обычной теплопроводностью, на внешней стороне этой области водяная пленка. На поверхности пленки поток электронов создает поверхностный заряд с плотностью связанный с нормальной компонентой электрического поля соотношением
Формула
Вследствие этого на единицу поверхности пленки действует сила
Формула
Где n - единичный вектор нормальный к поверхности. Отметим, что на плазменной поверхности двойного слоя напряженность электрического поля близка к нулю. Кроме того, на пленку действует сила поверхностного натяжения и давление внешнего нейтрального газа, которые также направлены во внутрь сфероида. Суммарное действие этих сил уравновешивается парциальным давлением электронного газа
Формула
где P0 - давление нейтрального газа и β0 - коэффициент поверхностного натяжения воды. Учитывая, что формулллла получим
формула
Суммарный заряд внешней оболочки приближенно равен нулю. В стационарном состоянии потоки электронов и ионов равны. Действие электрического поля в оболочке на ионы уравновешено достаточно большой силой трения (см. ниже). В результате сжатия плазмоида электростатическим давлением средняя плотность энергии в бессиловой области возрастает и при большой напряженности электрического поля приближенно равна формула . В результате плотность энергии в шаровой молнии может быть значительно больше предельной плотности энергии, установленной ранее на основании теоремы вириала [3].
Поступление газа в двойной электрический слой происходит в результате испарения молекул воды с поверхности пленки. Определенный вклад в этот процесс может дать неустойчивость заряженной пленки, находящейся в электрическом поле, относительно мелкомасштабных деформаций. Сечение взаимодействия ионов с кластером при низких температурах определяется кулоновским сечением, несмотря на его, относительно большой поперечный размер. Образование комплексных ионов приводит к снижению подвижности иона вследствие возрастания его массы. В результате этого вынос энергии ионами в окружающую среду существенно уменьшается. При изменении температуры пленки от 500C до 1000C упругость насыщенных паров воды возрастает от 92,5 мм.рт.ст. до атмосферного, что соответствует изменению плотности молекул воды приблизительно от 3*1018 см--3 до 2*1019 см--3. Образование гидратных оболочек вокруг иона при этих плотностях происходит за времена ~10-10 ÷10-11 сек. Плотность кластерной плазмы определяется балансом между поступлением в нее ионов и гибелью вследствие рекомбинации. В воздухе коэффициент рекомбинации кластеров достаточно велик. Однако скорость рекомбинации кластеров в плазме, находящейся в сильном электрическом поле, будет значительно меньше. Действительно, условие капли, содержащей разноименные заряды и находящейся в сильном электрическом поле, имеет вид:
Формула
сила кулоновского притяжения зарядов, E0 диэлектрическая постоянная воды, R1 расстояние между зарядами и R2 радиус капли. В (10) учтено, что дипольный электрический момент капли направлен вдоль вектора электрического поля. Поскольку в сильном электрическом поле первый член справа в уравнении (10) значительно больше силы поверхностного натяжения, то для равновесного расстояния между зарядами капли имеем
формула
Если расстояние между зарядами формула то капля разрывается внешним электрическим полем, поэтому RS определяет предельное, прицельное расстояние. Коэффициент рекомбинации, рассчитанный по приближенной схеме [10] формммула плотность частиц третьего сорта, и он значительно меньше его величины для свободной плазмы.
Плотность кластерной плазмы можно оценить из уравнения баланса частиц:
Форммммула
Где толщина оболочки кластерной плазмы. Если предположить, что третьей частицей является положительный или отрицательный кластер, то при напряженности электрического поля E=5*106 B/см, температуре пленки 500 С, σ = 3*10-3 см, R2 = Rs и потоке ионов в кластерную плазму Ni ui =1020 см-2 сек-1 для плотности кластеров получим из (12) N формула. Пробег иона в такой плазме порядка 6*10-9 см. Энергия, набираемая им в электрическом поле на длине свободного пробега, порядка 3*10-2 эВ. Потери энергии через ионный канал в этом случае относительно невелики.
Плотная плазма оболочки является отражательным экраном для интенсивного циклотронного излучения электронов из центральной области плазмоида. В результате частичного поглощения этого излучения поддерживается электронная температура в оболочке неизотермической плазмы. Вследствие различной скорости диффузии электронов и ионов центральная область плазмоида заряженна отрицательным зарядом. Шаровая молния обладает также электрическим и магнитным дипольными моментами, направленными вдоль ее оси симметрии.
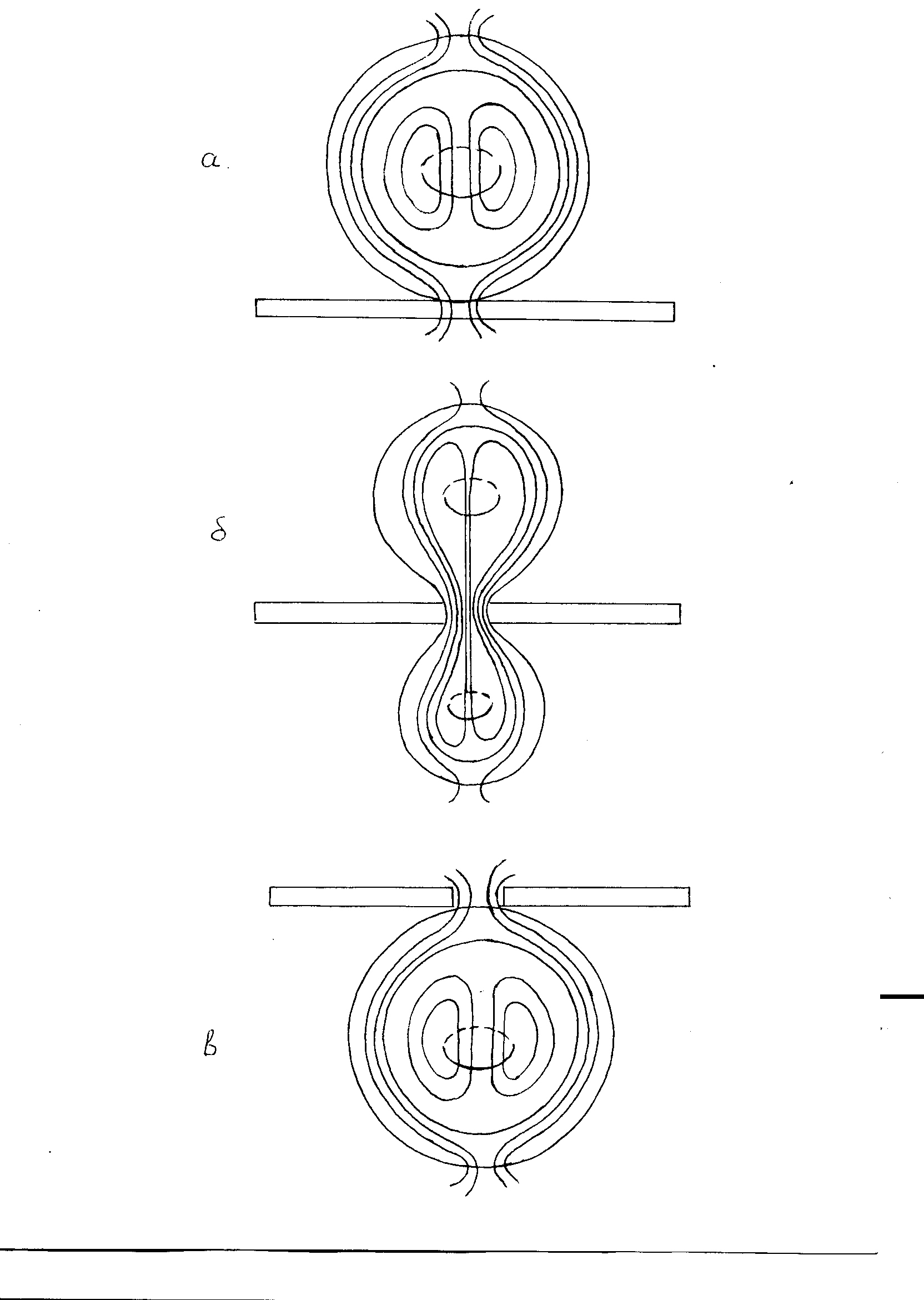
Перемещается она под действием силы тяжести, воздушных потоков и электромагнитных сил. Ее движение при малой электромагнитной силе сходно с двежением мыльного пузыря. В электрическом поле наведенного заряда в диэлектрике (стекле) она принимает такое положение, чтобы направление ее электрического дипольного момента совпадало с направлением поля. В результате она соприкасается со стеклом в области горловины ее внешнего магнитного поля. Захваченные частицы, уходящие вдоль силовых линий магнитного поля, расправляют стекло в этой области, проделывая в нем отверстие. Под действием разности давлений снаружи и внутри помещения шаровая молния переливается через это отверстие (см.Рис.4).
Основная энергия в
ней запасена в виде энергии магнитного поля. При форме плазмоида близкой к
форме шара его энергия W»H21R3/3. Время
жизни классического сферомака t = 2πσR2/![]() 2(4,5)2.
2(4,5)2.
Вес шаровой молнии определяется весом водяной пленки.
Взрыв шаровой молнии сопровождается генерацией мощного электромагнитного импульса. Она является источником интенсивного ренгеновского излучения. Основной вклад в излучение в видимом спектредает неизотермическая плазма оболочки. Наличие водяной пленки у шаровой молнии подтверждается наблюдением нескольких световых оттенков у нее, "экзотических" черных шаровых молний, а также особенностями ее движения. Голубой ореол вокруг шаровой молнии обусловлен рентгеновским и ультрафиалетовым излучением. Фиолетовое свечение вблизи ее границы вызывается электронами преодолевающеми пртенциальный барьер в двойном электрическом слое.
Наблюдение связанных шаровых молний, намагничевание металлических предметов и т.д. указывают на наличие у нее магнитного поля. В стадии угасания внешнее магнитное поле может отсутствовать [11].
Наиболее точно строение шаровой молнии описано в уникальном наблюдении М.Т.Дмитриева [12].
Заключение.
По грубым оценкам
плотность плазмы в центральной области шаровой молнии N~1019÷1014см-3,
T~104÷105эВ при времени жизни τ=
πσR2/10![]() 2~1÷10 сек.
Предельная напряженность электрического поля в двойном слое ~ 107В/см,
и, следовательно, плотность энергии в ней W=E2n/4π~10Дж/см-3.
Эта величин7а совпадает с величиной плотности энергии, установленной Стахановым
И.П. (3) на основе наблюдательных фактов. Таким образом, шаровая
молния может служить источником нейтронов, если заполнить её дейтерием или
другим термоядерным сырьём.
2~1÷10 сек.
Предельная напряженность электрического поля в двойном слое ~ 107В/см,
и, следовательно, плотность энергии в ней W=E2n/4π~10Дж/см-3.
Эта величин7а совпадает с величиной плотности энергии, установленной Стахановым
И.П. (3) на основе наблюдательных фактов. Таким образом, шаровая
молния может служить источником нейтронов, если заполнить её дейтерием или
другим термоядерным сырьём.
На основе данной модели удаётся дать удовлетворительное описание поведения шаровой молнии в различных условиях.
Иллюстрации
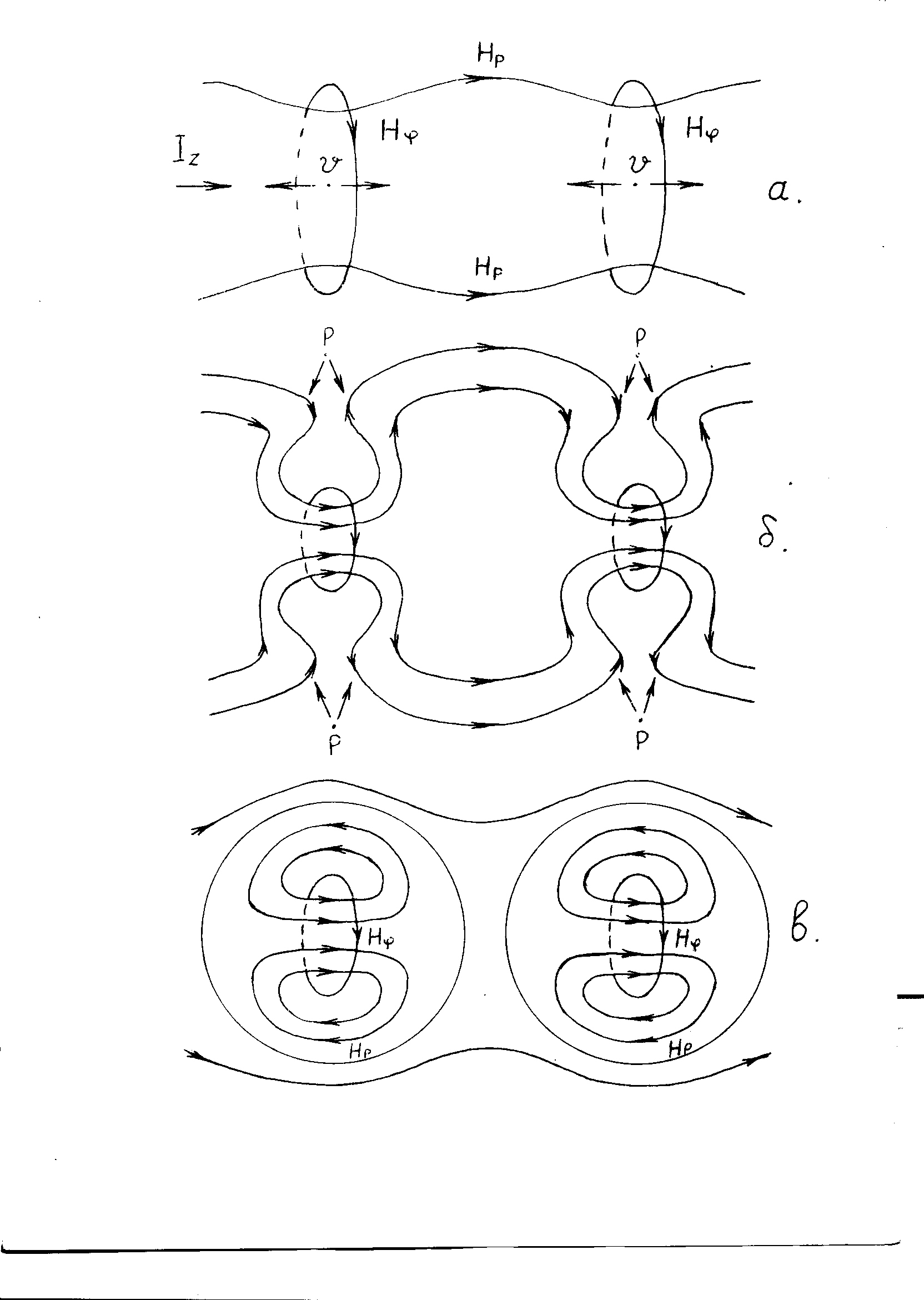
Рисунок 1.
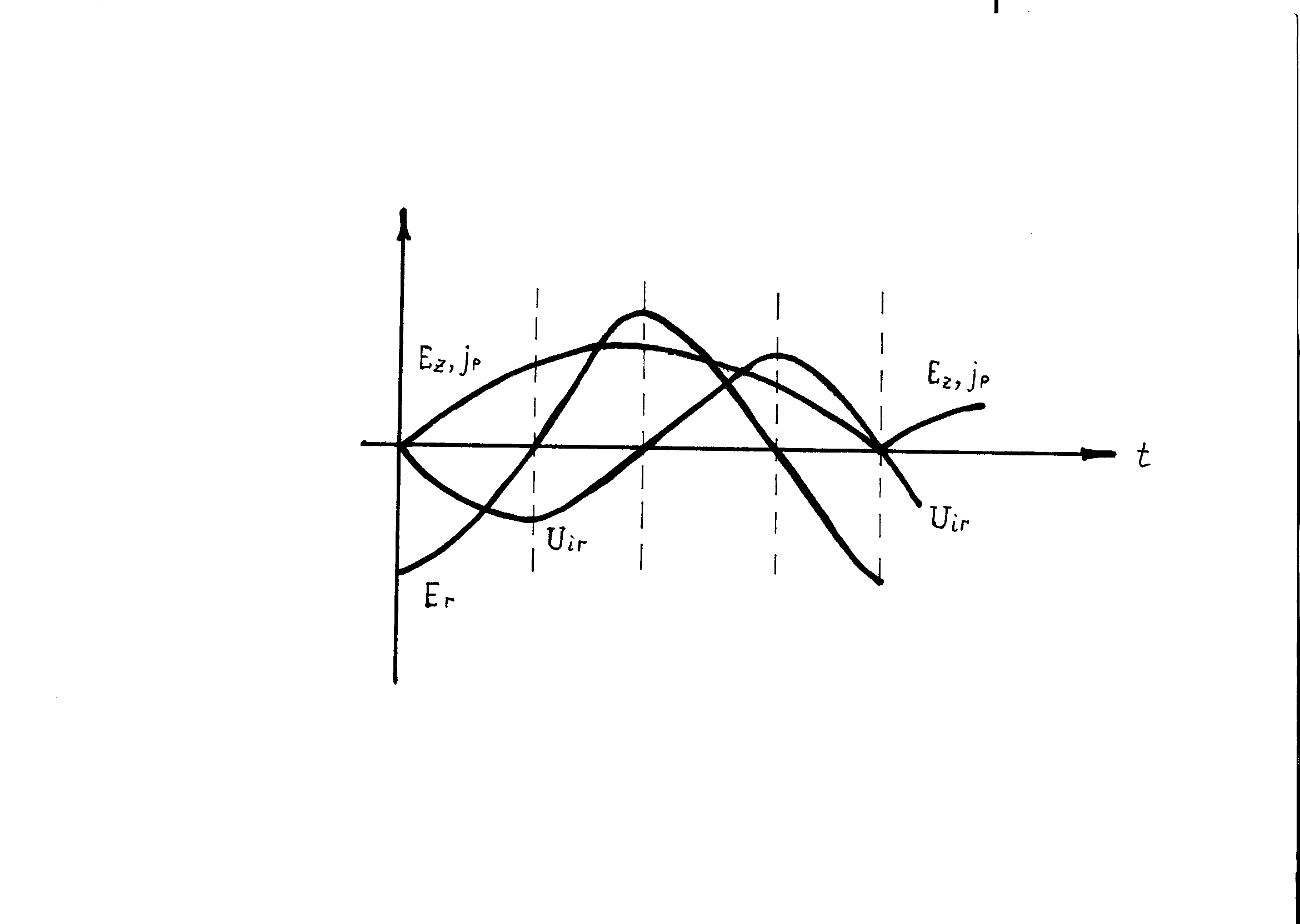
Рисунок 2.
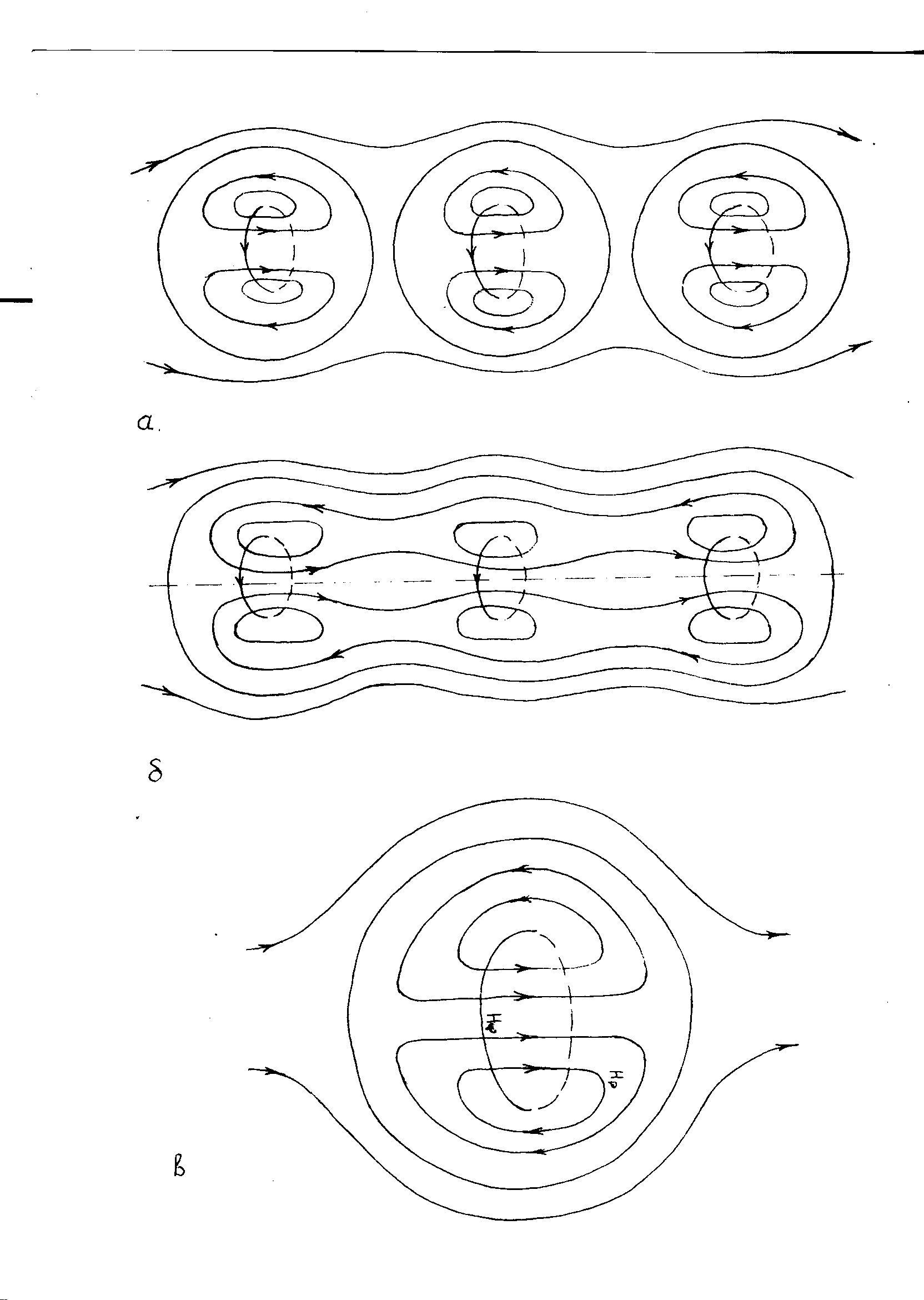
Рисунок 3.
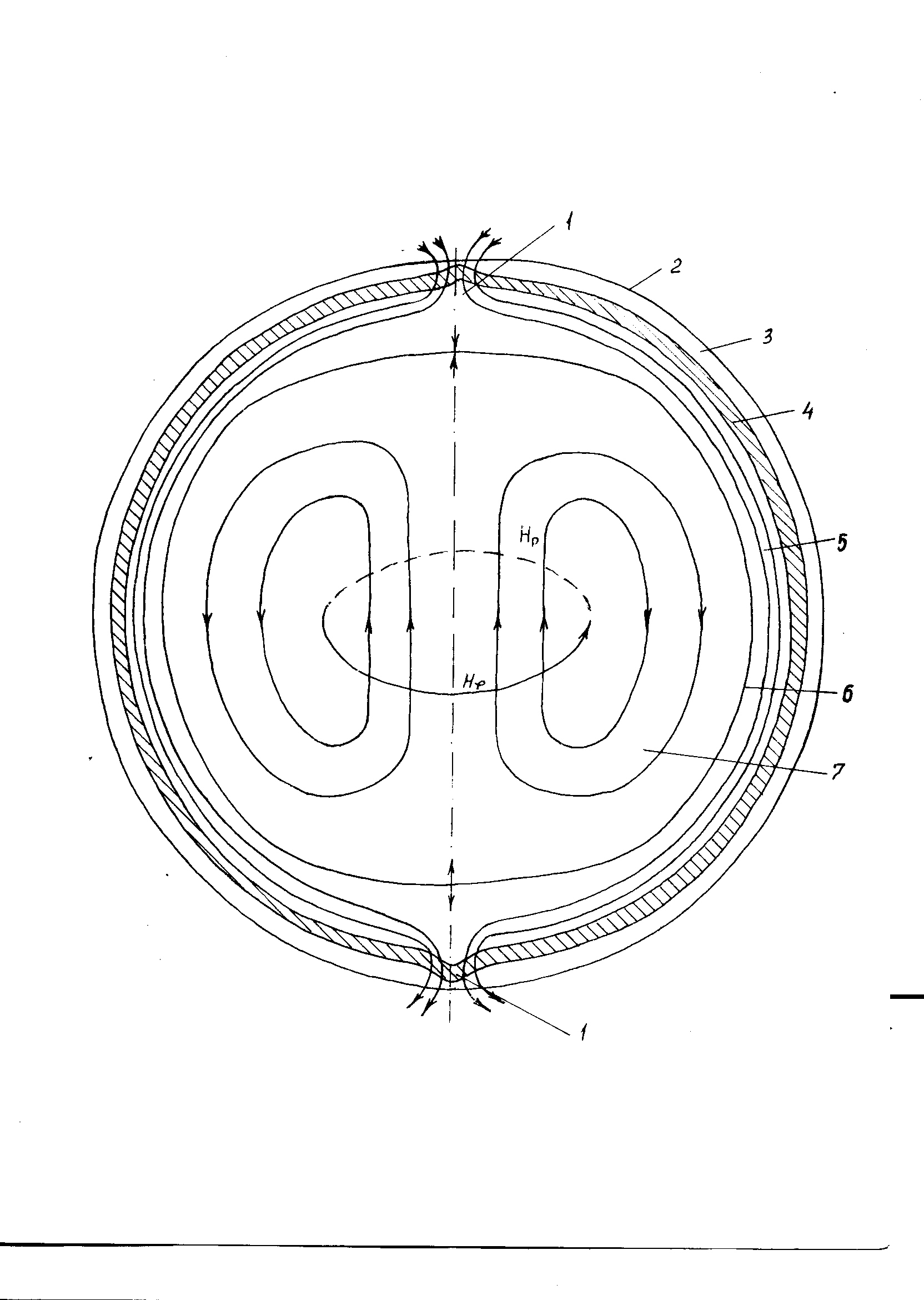
1 – горловина внешнего магнитного поля.
2 – водяная плёнка.
3 – двойной электрический слой.
4 – оболочка неизотермической плазмы.
5 – переходной токовый слой.
6 – сепаратриса.
7 – область бессилового магнитного поля.
Рисунок 4.
Литература.
1. А.Ф. Попов. Тезисы докладов 24 Звенигородской конференции по физике плазмы и УТС. Февраль 1997, стр.237.
3. И.П. Стаханов. О физической природе шаровой молнии. Энергоатомиздат, Москва, 1985.
12. М.Т. Дмитриев. Природа 6,
стр.98, 1967.
